Quantification of dynamic structural changes of nanomaterials via atom-counting from sequential ADF STEM images

Session

Stream 2: EMAG - Automated Control, Advanced Data Processing

Authors

Annelies De wael (3, 5), Annick De Backer (3, 5), Lewys Jones (1, 6), Aakash Varambhia (4), Peter Nellist (2), Sandra Van Aert (3, 5)

Affiliations

1. Advanced Microscopy Laboratory, CRANN
2. Department of Materials, University of Oxford
3. EMAT, University of Antwerp
4. Johnson Matthey Technology Centre, Sonning Common
5. NANOlab Center of Excellence, University of Antwerp
6. School of Physics, Trinity College Dublin, The University of Dublin

Keywords

• atom-counting
• dynamic structural changes
• open source software
• quantitative electron microscopy 
• scanning transmission electron microscopy

Abstract text

We present a new method which allows us to reliably quantify dynamic changes in the atomic structure of nanomaterials using a time series of high-resolution annular dark field scanning transmission electron microscopy (ADF STEM) images [1,2]. The approach allows us to count the number of atoms in the atomic columns of a monatomic nanostructure in each frame of an ADF STEM time series using a hidden Markov model. We demonstrate improved reliability as compared to existing single-frame counting procedures. Furthermore, the method can be used to estimate the probability and cross-section for dynamic processes such as surface diffusion, adatom dynamics, beam effects, or structural changes during in situ experiments.

Quantitative analysis of atomic resolution electron microscopy images is commonly used to study the atomic structure of a nanomaterial. When such quantitative analysis is applied to a stationary structure, the insight into the dynamics is lacking. The atomic structure of nanomaterials can change over time via adatom dynamics, surface diffusion, beam effects, or during in situ experiments. Therefore, we propose a quantitative approach specifically designed to analyse the dynamically changing atomic structure using a time series of ADF STEM images [1,2]. A useful quantity for retrieving this atomic structural information is the so-called scattering cross-section, a measure for the total intensity of electrons scattered towards the annular detector from an atomic column [3,4]. The scattering cross-section increases with increasing atomic mass number Z and thickness in ADF STEM. Therefore, in pure-element nanomaterials, the number of atoms in each atomic column can be determined using these scattering cross-sections [5-11]. To quantify the dynamic changes in the number of atoms in each atomic column, we use a so-called hidden Markov model (HMM) [12]. HMMs are widely used in other fields of science owing to their optimal properties for modelling and analysing time series data. We apply HMMs to ADF STEM data for the first time.

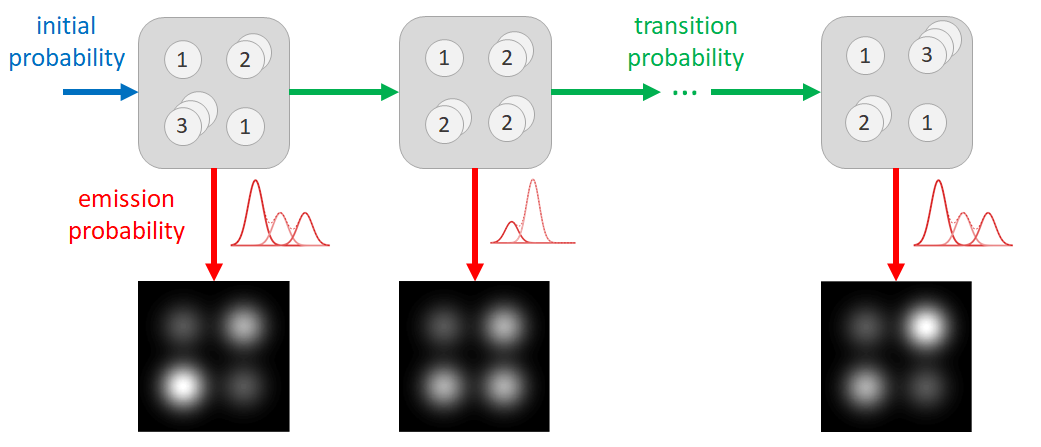
A HMM consists of two layers: a “hidden" Markov chain state sequence and an observed sequence, schematically represented in Fig. 1. In the case of atom-counting, the “hidden” states are the number of atoms in each atomic column at the different times, observed only indirectly through the series of ADF STEM images. The observed sequence consists of the scattering cross-sections for each atomic column in each image. The changes in the number of atoms (hidden states) are described as a discrete set of transition probabilities. At each time, scattering cross-sections (observations) result from the underlying number of atoms (hidden states) following an emission probability, here described by a Gaussian distribution. The parameters of the HMM are estimated using a Baum-Welch algorithm, followed by a Viterbi path backtracking algorithm to determine the most likely state sequence [12-14].

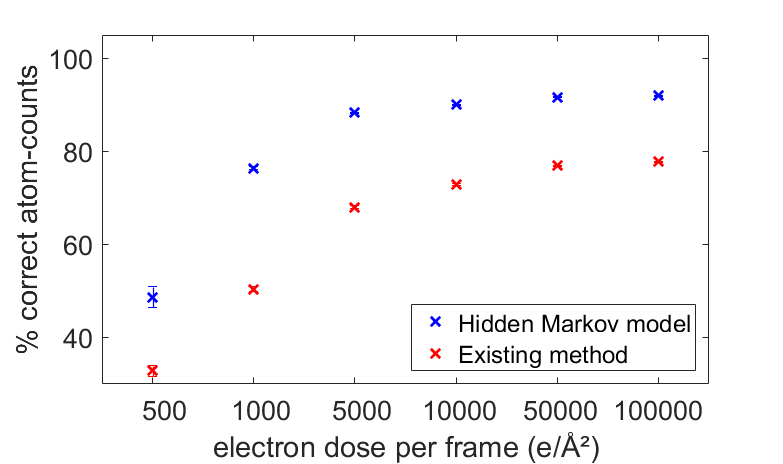
The benefit of this new approach for atom-counting from a time series of ADF STEM series is illustrated in Fig. 2. We simulated scattering cross-sections corresponding to hypothetic ADF STEM time series with 40 frames of a changing Pt nanoparticle with 215 atomic columns, and a thickness up to 15 atoms. The number of atoms in a column can change by +/- 1 from frame to frame throughout the time series, with a probability of 10%. The atom-counting performance is compared with the existing atom-counting approach based on a single-frame analysis. The HMM far exceeds the atom-counting reliability of the existing methods, thanks to the embedding of transition probabilities which explicitly model atomic structural changes.

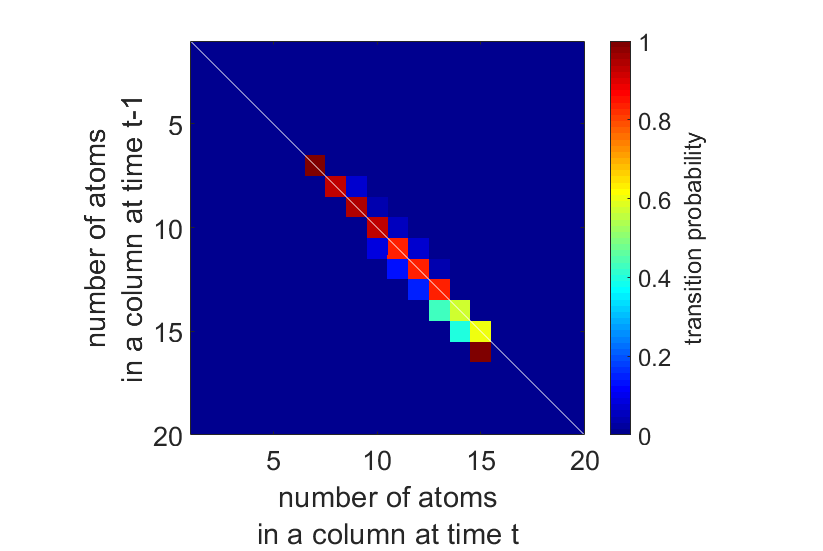
Next, we apply this to an experimental time series of a Pt wedge, shown in Fig. 3. The dynamic structural changes are summarised by the transition probabilities, displayed in Fig. 4. The white diagonal line plotted on top of the transition matrix indicates the transitions where the number of atoms in an atomic column stays the same. The upper and lower triangles contain the probabilities for an atomic column to respectively gain or lose one or more atoms. We do not expect structural changes to be caused by sputtering of atoms from the surface, only by surface diffusion, since the threshold energy for sputtering Pt atoms from a convex surface with step sites is 379 keV, well above the incident electron energy of 300 keV [15,16]. The HMM analysis enables us to quantify the probability for surface diffusion from this time series. We estimate the average probability for a surface atom to move to another column equal to 6.3%. We can even determine an experimental value for the average cross-section for surface diffusion, σ=5.60 x 10^-6 Ų, which corresponds to a surface diffusion threshold energy of 1.09 eV, in close agreement with the theoretical value of 1.07 eV [17]. 

In conclusion, we present a new framework to reliably count the number of atoms in the atomic columns of a monatomic nanostructure in each frame of an ADF STEM time series using a hidden Markov model. We show that the performance of this new method significantly surpasses that of the current method for atom-counting. Furthermore, we interpret the transition probabilities in terms of a probability and cross-section for surface diffusion. The hidden Markov model for atom-counting therefore holds promise for a reliable quantification of dynamic structural changes by adatom dynamics, surface diffusion, beam effects, or during in situ experiments. The HMM was implemented in the freely available StatSTEM software [7].

 

Figure 1. The hidden Markov model for atom-counting models the number of atoms in each atomic column of the nanoparticle as the hidden states (top row) and the scattering cross-sections obtained from the ADF STEM images as the observations (bottom row). Hidden states and observations are connected through the emission probability (red). The hidden states change according to initial (blue) and transition probabilities (green).

 

Figure 2. Percentage of correctly counted atomic columns, with 95% confidence intervals, as a function of the electron dose in each individual frame.

 

Figure 3. (a) Experimental ADF STEM time series of a Pt wedge. (b) From the estimated hidden Markov model, the hidden state sequence is retrieved.

Figure 4. Transition matrix estimated by the hidden Markov model for the Pt wedge in Fig. 3.

References

References

[1] A. De wael et al., Physical Review Letters 124 (2020), 106105.

[2] A. De wael et al., Ultramicroscopy 219 (2020), 113131

[3] S. Van Aert et al., Ultramicroscopy 109 (2009), 1236.

[4] H. E et al., Ultramicroscopy 133 (2013), 109.

[5] S. Van Aert et al., Nature 470 (2011), 374.

[6] A. De Backer et al., Ultramicroscopy 134 (2013), 23.

[7] S. Van Aert et al., Physical Review B 87 (2013), 064107.

[8] A. De Backer et al., Ultramicroscopy 171 (2016), 104.

[9] J. M. LeBeau et al., Nano Letters 10 (2010), 4405.

[10] L. Jones et al., Nano Letters 14 (2014), 6336.

[11] A. De wael et al., Ultramicroscopy 177 (2017), 69.

[12] L. R. Rabiner, Proceedings of the IEEE 77 (1989), 257.

[13] A. J. Viterbi, IEEE Transactions on Information Theory 13 (1967), 260.

[14] G. D. Forney, IEEE Transactions on Information Theory 61 (1973), 268.

[15] R. F. Egerton et al., Ultramicroscopy 110 (2010), 991-997.

[16] S. Van Aert et al., Physical Review Letters 122 (2019), 066101.

[17] T. Halicioglu et al., Thin Solid Films 57 (1979), 241-245. 

[18] This project has received funding from the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation programme (Grant Agreement No. 770887 and No. 823717 ESTEEM3). The authors acknowledge financial support from the Research Foundation Flanders (FWO, Belgium) through grants to A.D.w. and A.D.B. and projects G.0502.18N and EOS 30489208. L.J. acknowledges the SFI AMBER Centre for support. A.V. and P.D.N. acknowledge the UK Engineering and Physical Sciences Council (EPSRC) for support (EP/K040375/1 and 1772738). A.V. also acknowledges Johnson-Matthey for support.